
Theory of Complex Systems Department
Marian Smoluchowski Institute of Physics
Jagiellonian University
Dr Jakub Gizbert-Studnicki
SONATA grant
Impact of topology on phase structure of quantum gravity in Causal Dynamical Triangulations

Project description
Causal Dynamical Triangulations (CDT) is a nonperturbative approach to quantum gravity based on Feynman's path integral. Formal integral over geometries is
defined and regularized by a lattice discretization of spacetime in a form of triangulation constructed from four-dimensional simplices. Final length of lattice
links constitutes an ultraviolet cutoff which can be, in principle, removed in the continuum limit connected with higher order phase transitions.
Investigation of CDT phase structure and order of the phase transitions is a first step toward finding this limit. It is also important that quantum gravity
should be able to correctly reproduce the infrared limit compatible with Einstein's General Relativity.
The key assumption of CDT is an introduction of a proper time foliation of spacetime into spatial hypersurfaces of constant topology, which cannot be changed
in time evolution. Previous research of CDT were mostly done for spatial topology of a 3-sphere (S3) and time periodic boundary conditions
(spacetime topology: S1 x S3). In such topological conditions CDT has a rich phase structure (four phases were discovered). A very promising result is the existence
of phase transitions of higher order and a dynamical emergence of semiclassical background geometry consistent with General Relativity in one of the phases.
The objective of the research project is a study of the impact of spatial topology change on CDT phase structure. The study concerns spatial topology
of a 3-torus (T3). Preliminary results suggest that a semiclassical phase exists but it has different geometry than the semiclassical phase observed for the 3-sphere
topology. The existence of other phases and the order of phase transitions are open questions.
The research will employ methods developed in the frameworks of general relativity, quantum field theory, lattice field theory, renormalization group and computer science.
The research in four-dimensional CDT is mostly based on Monte Carlo numerical simulations. The Monte Carlo algorithm has been successfully
implemented as a computer program in C. The program has been tested and used in previous studies of CDT. Computer simulations will be performed by supercomputer SHIVA
in Mark Kac Center for Complex Systems Research, Jagiellonian University, and computer cluster of Theory of Complex Systems Department in the Institute of Physics,
Jagiellonian University.
The project focuses on novel and yet not solved issues concerning the theory of quantum gravity. Due to experimental limits (ultra high energies) the studies of quantum gravity
are mostly based on theoretical approaches. CDT is an approach which may lead to a better understanding of spacetime properties in ultra small scales.
The project will be conducted in international cooperation with researchers from Niels Bohr Institute (Copenhagen, Denmark) and Radboud University (Nijmegen, Netherlands).
Main project themes
- Preparation of the phase diagram: the phase space of CDT coupling constants will be scanned in a search of various phases of quantum geometry and approximate position of phase transition lines.
- Investigation of the order of phase transitions: order parameters will be constructed and analyzed to establish precise position and order of phase transitions.
- Investigation of the impact of introducing matter fields: minimally coupled scalar fields will be introduced to CDT. The results will be compared to the effect of scalar fields in 3-sphere spatial topology.
Publications
- The phase structure of causal dynamical triangulations with toroidal spatial topology
J. Ambjorn, J.Gizbert-Studnicki, A. Gorlich, J.Jurkiewicz, D. Nemeth, Journal of High Energy Physics, 06 (2018) 111, [JHEP06(2018)111].
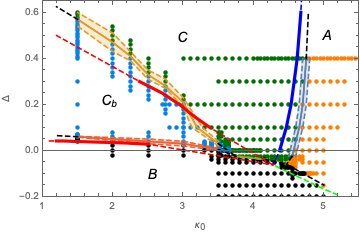
We investigate the impact of topology on the phase structure of fourdimensional Causal Dynamical Triangulations (CDT). Using numerical Monte Carlo simulations we study CDT with toroidal spatial topology. We confirm existence of all four distinct phases of quantum geometry earlier observed in CDT with spherical spatial topology. We plot the toroidal CDT phase diagram and find that it looks very similar to the case of the spherical spatial topology.
- Pseudo-Cartesian coordinates in a model of Causal Dynamical Triangulations
J. Ambjorn, Z. Drogosz, J. Gizbert-Studnicki, A. Gorlich, J. Jurkiewicz, Nuclear Physics B, 943 (2019) 114626, [NuclPhysB(2019)114626].
Causal Dynamical Triangulations is a non-perturbative quantum gravity model, defined with a lattice cut-off. The model can be viewed as defined with a proper time but with no reference to any three-dimensional spatial background geometry. It has four phases, depending on the parameters (the coupling constants) of the model. The particularly interesting behavior is observed in the so-called de Sitter phase, where the spatial three-volume distribution as a function of proper time has a semi-classical behavior which can be obtained from an effective mini-superspace action. In the case of the three-sphere spatial topology, it has been difficult to extend the effective semi-classical description in terms of proper time and spatial three-volume to include genuine spatial coordinates, partially because of the background independence inherent in the model. However, if the spatial topology is that of a three-torus, it is possible to define a number of new observables that might serve as spatial coordinates as well as new observables related to the winding numbers of the three-dimensional torus. The present paper outlines how to define the observables, and how they can be used in numerical simulations of the model.
- Towards an UV fixed point in CDT gravity
J. Ambjorn, J. Gizbert-Studnicki, A. Gorlich, J. Jurkiewicz, D. Nemeth, Journal of High Energy Physics, 07 (2019) 166, [JHEP07(2019)166].
CDT is an attempt to formulate a non-perturbative lattice theory of quantum gravity. We describe the phase diagram and analyse the phase transition between phase B and phase C (which is the analogue of the de Sitter phase observed for the spherical spatial topology). This transition is accessible to ordinary Monte Carlo simulations when the topology of space is toroidal. We find that the transition is most likely first order, but with unusual properties. The end points of the transition line are candidates for second order phase transition points where an UV continuum limit might exist.
- Critical phenomena in causal dynamical triangulations
J. Ambjorn, D.Coumbe, J. Gizbert-Studnicki, A. Gorlich, J. Jurkiewicz, Classical and Quantum Gravity, 36 (2019) 224001, [arXiv:1904.05755].
Four-dimensional CDT (causal dynamical triangulations) is a lattice theory of geometries which one might use in an attempt to define quantum gravity non-perturbatively, following the standard procedures of lattice field theory. Being a theory of geometries, the phase transitions which in usual lattice field theories are used to define the continuum limit of the lattice theory will in the CDT case be transitions between different types of geometries. This picture is interwoven with the topology of space which is kept fixed in the lattice theory, the reason being that "classical" geometries around which the quantum fluctuations take place depend crucially on the imposed topology. Thus it is possible that the topology of space can influence the phase transitions and the corresponding critical phenomena used to extract continuum physics. In this article we perform a systematic comparison between a CDT phase transition where space has spherical topology and the "same" transition where space has toroidal topology. The "classical" geometries around which the systems fluctuate are very different it the two cases, but we find that the order of phase transition is not affected by this.
Funding
This research is funded by the National Science Centre, Poland, through the project SONATA 12 number 2016/23/D/ST2/00289.