
Theory of Complex Systems Department
Institute of Theoretical Physics
Jagiellonian University
Quantum Gravity and Cosmology
Unifying quantum theory with general relativity to form a complete and predictive theory of quantum gravity is one the great outstanding challenges of modern physics. Here, at the Institute of Theoretical Physics our ambitious aim is to achieve this unification via an approach known as Causal Dynamical Triangulations (CDT). A key strength of CDT is the simplicity of construction: we assume only the central principles of Quantum Theory and General Relativity, including few additional ingredients. CDT models continuous spacetime via the connectivity of an ensemble of locally flat d-dimensional triangular building blocks. In close analogy to the sum over all possible paths in Feynman's path integral approach to Quantum Mechanics, CDT sums over all allowed spacetime geometries. A central feature of CDT is the foliation of spacetime into space-like hypersurfaces of fixed topology.
Analytical methods in 4-dimensional Causal Dynamical Triangulations have thus far proved intractable due to the complex nonperturbative sum over geometries. However, with the advent of powerful computational tools, numerical approaches to dynamical triangulations can now be successfully employed via Monte Carlo simulations. Due to this fact the implementation of our research is predominately numerical and utilizes a computational cluster and network of computer nodes within the department.
Despite the simplicity of construction, or perhaps because of it, CDT has produced a number of important results and conceptual insights, and is now widely regarded as a serious contender for a nonperturbative and background independent theory of Quantum Gravity. Some of the successes of the CDT approach include evidence for a classical limit that closely resembles general relativity on large distance scales, while on short distance scales it has yielded some exciting clues as to the nature of space-time at the Planck scale. In particular, there is evidence that 4-dimensional space-time dynamically emerges on large distance scales from a lower dimensional geometry at the Planck scale. This intriguing phenomenon, known as dimensional reduction, has since been observed in a number of other approaches to Quantum Gravity and is an active field of research.
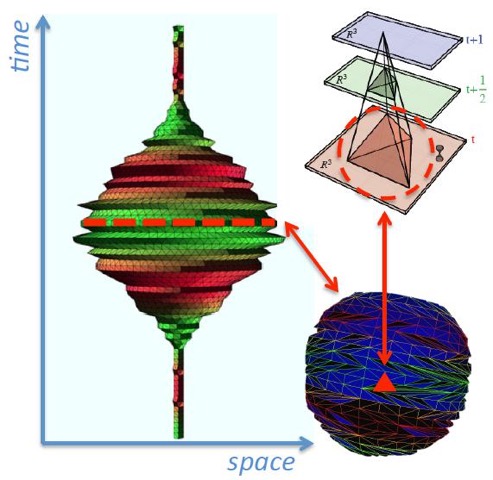
Although CDT has enjoyed a number of successes, of course many questions still remain. Does CDT have a well defined continuum limit? Can CDT help us to understand whether dimension and metric signature are fixed or dynamical quantities? Is the introduction of a causality condition via the foliation of space-time an essential ingredient in the formulation of quantum gravity, or can this condition be relaxed? Can CDT help us to understand other approaches to quantum gravity such as Horava-Lifshitz gravity, Loop Quantum Cosmology or asymptotically safe gravity? And ultimately, how can we successfully unite quantum theory with General Relativity? Our research group is actively pursuing answers to these important questions.
For information about recent research projects within this area, please visit http://cs.if.uj.edu.pl/atg/grants/sonata.html and http://cs.if.uj.edu.pl/jstud/JGSSonata.html. Principal investigators: prof. dr hab. Jerzy Jurkiewicz, dr hab. Andrzej Görlich, dr hab. Jakub Gizbert-Studnicki.
Quantum Cosmos Lab
Quantum Cosmos Lab is an interdisciplinary research team exploring physics at the interface between quantum mechanics and the theory of gravity. Our activity is mainly devoted to fundamental studies within theoretical physics and cosmology. However, we also link this theoretical research to advanced technologies, such as quantum computing, quantum communication and space technologies.
The main areas of our research are: - Quantum gravity and quantum cosmology - Nonlinear phase space field theories - Phenomenology of quantum gravity - Simulations of quantum gravity on quantum computers - Gravity/entanglement duality - Theoretical foundations of quantum space communication - Classical and quantum cryptology

Website and social media: https://quantumcosmos.org/, https://twitter.com/QuantCosm. PI: dr hab. Jakub Mielczarek.
String Theory and AdS/CFT correspondence
The AdS/CFT correspondence is an equivalence (or duality) between (supersymmetric) gauge theory and superstring theory in a specific curved 10-dimensional spacetime. The equivalence between the two kinds of theories means that physical problems in one theory can be translated into problems within the framework of the other theory. One should stress that the equivalence of such completely different theories is fascinating theoretically. Due to the fact that the gauge theory can be understood as living on the boundary of the higher dimensional curved spacetime, the equivalence of the two theories is often referred to as holography.
This duality enables us to study the most elusive and difficult nonperturbative regime of gauge theory, as then the dual superstring theory reduces essentially to higher dimensional gravity. One can then translate various dynamical questions in gauge theory into geometrical properties of the dual gravitational theory. As an example, static uniform gauge theory plasma is mapped to a 5D black hole, and the temperature and entropy are mapped respectively to the Hawking temperature and area of the horizon. Dynamics and temporal evolution is mapped to the 5D Einstein's equations with appropriate matter fields.
Research in our group involves the study of strongly interacting gauge theory plasma using these holographic methods, concentrating especially on far from equilibrium behaviour, the transition to a hydrodynamic description and the dynamics of phase transitions. Apart from these more applied research directions, we are also interested in understanding the origins of holography and the emergence of the higher dimension gravitational description directly from the boundary field theory.
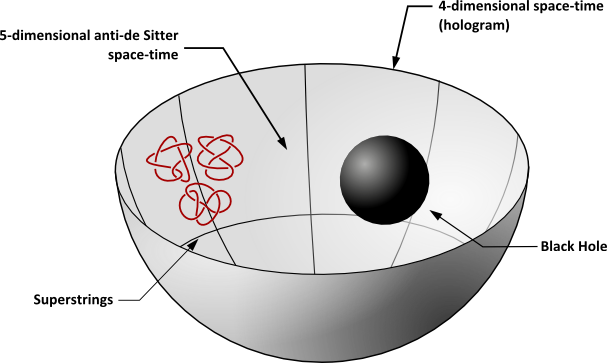
image source: quantum bits
For more information about research performed within the project "From string theory to gauge theory - the AdS/CFT correspondence", see http://cs.if.uj.edu.pl/projects/adscft/.
The NCN funded project Holographic connections between quantum fields, information, and gravity led by Dr. Mario Flory started in September 2022 and will run for a duration of 5 years. Topics to be studied in the course of this project include Quantum Information aspects of AdS/CFT (such as entanglement entropy and notions of complexity), applications of AdS/CFT to quantum field theory and condensed matter physics, and foundations of the holographic principle.
Principal investigators: Prof. Romuald Janik, Dr. Hesam Soltanpanahi and Dr. Mario Flory.
Random Matrix Theory
One can look at random matrix theory (hereafter RMT) as an alternative to classical probability calculus, where instead of single random variable we have to deal with a huge set of random numbers arranged in a matrix-like structure. Such construction is not only possible, but it shares amazing similarities to classical probability calculus. Moreover, this correspondence can be formalized at the mathematical level in the case where the size of the random matrix tends to infinity. By no means this is a severe restriction, since in contemporary applications the sizes of random matrices can easily reach the order of 10^4 (financial engineering), 10^7 (wireless networks) or even 10^10 (genetics). So, almost paradoxically, the bigger the size of the random matrix, the more definite prediction we can make on its statistical properties.
The cornerstone of this new calculus of large matrices is the study of the spectra (eigenvalues) of the matrices. Alike in a classical probability calculus, powerful central limit theorems exist in random matrix theory. This is the reason, why so many similar, macroscopic spectral properties are shared by diverse and unrelated complex random systems (in analogy to the ubiquitous Gaussian distribution in single-valued random structures). We call this phenomenon macroscopic universality of RMT. Macroscopic - as a distinction from the so-called microscopic universality of RMT, a second powerful phenomenon responsible for the wide scope of applications of RMT. Microscopic universality of RMT is the consequence of interactions between the eigenvalues. Since this interaction is long-ranged, certain critical spectral phenomena can emerge locally at the vicinity of some points of the spectra of the matrices. The spectral behavior in the vicinity of these points (fluctuations) depends usually only on the symmetries of the system, therefore can be categorized into universality classes, shared by very different complex systems respecting the underlying symmetry of the matrix model.
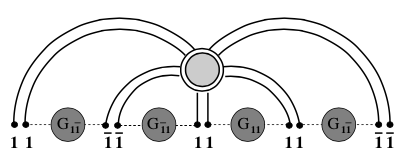
Random matrix theory (and in particular its version known as Free Random Variables) can be therefore described as the probability calculus of the XXI century. Nowadays, it is hard to find a branch of science where it does not have any applications.
For more information about research performed within the project "Interdisciplinary applications of Random Matrix Theory", see http://th.if.uj.edu.pl/~mrmt/. Principal investigator: prof. dr hab. Maciej Nowak.
Data Science, Machine Learning and the study of Complex Systems
The artificial neural network model was created based on analogies to biological counterparts, such as a simplified model of the neuron or a system of retinal neurons. Due to the increasing complexity of tasks and problems with the development of effective methods for learning deep neural networks, solutions based on algebraic structures dominate. Today, advanced approaches in machine learning such as deep learning show a number of undesirable features, such as forgetfulness, susceptibility to adversarial examples, the requirement for a large training set, and slow learning. Most of these features do not occur in biological systems, thus it would be beneficial to take an inspiration from them to help training artificial systems. The aim of the project is to analyze high-level behaviors of biological neural systems and to build innovative artificial models by proposing new paradigms of learning and new architectures of computational models.

image source: starline / Freepik
For more information about the ongoing bioNN project, see http://bionn.matinf.uj.edu.pl. Principal investigators: prof. dr hab. Maciej Nowak, dr hab. Paweł Oświęcimka, prof. dr hab. Romuald Janik.
Biophysics of developmental systems
The development of multicellular organism is a remarkably reproducible process. Cells are exposed to chemical cues that pattern tissues to specify regions of different cell types that will later on give rise to distinct body parts. Interestingly, the noisy signalling events are interpreted to establish cell fate with striking precision of a few cell diameters. How such remarkable precision is achieved is a fundamental question in biology that is still poorly understood.
We focus on unravelling biophysical mechanisms that result in the remarkably precise formation of gene expression patterns (cell fates) in developing organisms. We address the following questions: How is information decoded in developmental systems? What types of regulatory mechanisms enhance patterning precision? How does feedback between source and target tissue alter pattern reproducibility? To address these questions, we combine methods from theoretical physics with data driven analysis. Using theoretical methods, we construct models by combining general principles of morphogen production and spreading, with various mechanisms of interpretation of morphogen signalling by cells undergoing specification. In the data-driven approach, we use computational methods to constrain models with high-resolution spatiotemporal data of spinal cord formation obtained from experimental labs. By using these two complementary approaches we aim to understand the design principles of regulatory mechanisms that result in precise and reproducible pattern formation in a wide range of developmental systems.
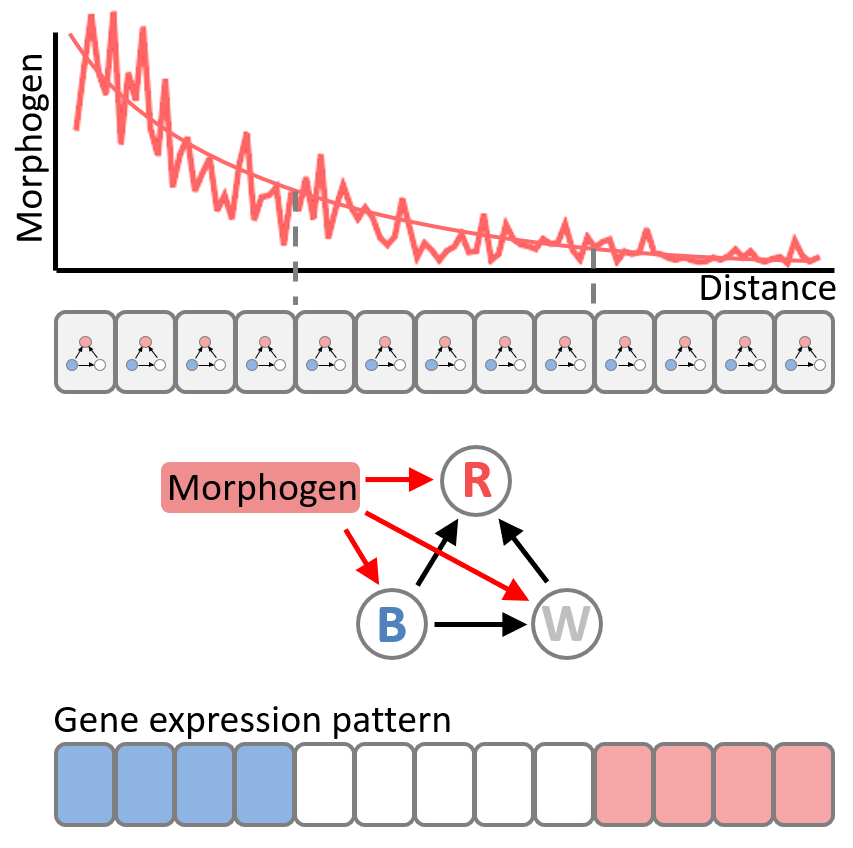
We also develop computational tools that facilitate exploration of multidimensional space of regulatory networks or genotypes to find solutions with the highest fitness against imposed functional goals.
More information at https://zagorskigroup.com/research/. Principal investigator: dr Marcin Zagórski.
Other (related) areas of research
- Quantum Chromodynamics
- Network Theory
- Econophysics
- Mathematical methods of theoretical physics applied to interdisciplinary problems
- ...