
Theory of Complex Systems Department
Marian Smoluchowski Institute of Physics
Jagiellonian University
Dr Piotr Warchoł
SONATA grant
Random Matrices and Information Measures

Project description
The goal of the project is to further the understanding of random matrix theory related problems by
assuming an information-theoretic perspective. The idea is that the border between those two areas
will prove to be a fruitful ground for new discoveries in statistical and complex systems physics. We
will particularly explore three topics emerging in that context: universal probability distributions
and phase transitions in random matrix related complex systems (and their relation to information
theoretic measures) and the data analysis methods fusing the tools from the two subjects.
Random Matrix Theory emerges in the description of many, very different, physical systems. This is
a consequence of universality and the fact that it is basically a probability theory for noncommuting random variables.
In some sense, in the context of many physical applications,
it also represents an exercise in finding and solving a mathematical model that will mimic some particular
phenomena but which carries the least amount of information under some constraints.
Information theory is nowadays energetically studied not only for the benefit of its applications but
also due to the fundamental role entropy plays in most of physics. For example, new information
related measures have been designed and studied with the aim of quantifying the processes
occurring in a vast array of complex systems.
The project will have an impact by broadening the knowledge in the two fields, and wider, in
theoretical physics.
Main project themes
- Random Matrix Theory probability distributions in light of Information Theory.
- Phase transitions in systems adhering a random matrix description with the modern tools of Information Theory.
- Application of methods combing Random Matrix Theory and Information Theory to data and complex systems analysis.
Publications
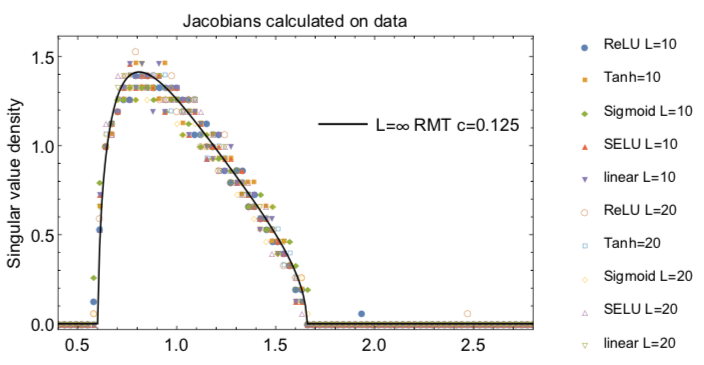
- Dynamical Isometry is Achieved in Residual Networks in a Universal Way for any Activation Function
W. Tarnowski, P. Warchoł, S. Jastrzębski, J. Tabor, M. A. Nowak, accepted to AISTATS 2019, [arXiv:1809.08848].
We demonstrate that in residual neural networks (ResNets) dynamical isometry is achievable irrespective of the activation function used. We do that by deriving, with the help of Free Probability and Random Matrix Theories, a universal formula for the spectral density of the input-output Jacobian at initialization, in the large network width and depth limit. The resulting singular value spectrum depends on a single parameter, which we calculate for a variety of popular activation functions, by analyzing the signal propagation in the artificial neural network. We corroborate our results with numerical simulations of both random matrices and ResNets applied to the CIFAR-10 classification problem. Moreover, we study consequences of this universal behavior for the initial and late phases of the learning processes. We conclude by drawing attention to the simple fact, that initialization acts as a confounding factor between the choice of activation function and the rate of learning. We propose that in ResNets this can be resolved based on our results by ensuring the same level of dynamical isometry at initialization.
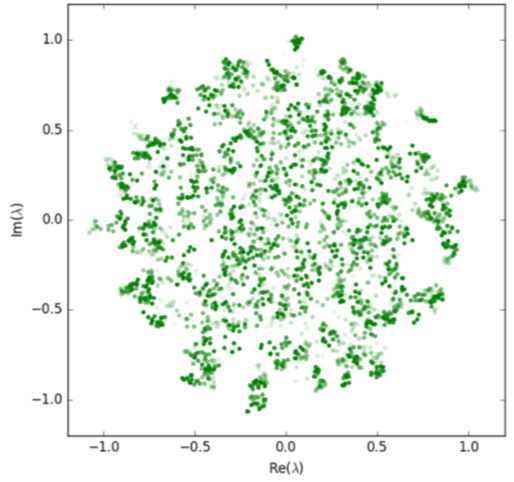
- Full Dysonian dynamics of the complex Ginibre ensemble
J. Grela, P. Warchoł,JOURNAL OF PHYSICS A: MATHEMATICAL AND THEORETICAL, 51, 425203, [arXiv:1804.09740].
We find stochastic equations governing eigenvalues and eigenvectors of a dynamical complex Ginibre ensemble reaffirming the intertwined role played between both sets of matrix degrees of freedom. We solve the accompanying Smoluchowski–Fokker–Planck equation valid for any initial matrix. We derive evolution equations for the averaged extended characteristic polynomial and for a class of k-point eigenvalue correlation functions. From the latter we obtain a novel formula for the eigenvector correlation function which we inspect for Ginibre and spiric initial conditions and obtain macro- and microscopic limiting laws.
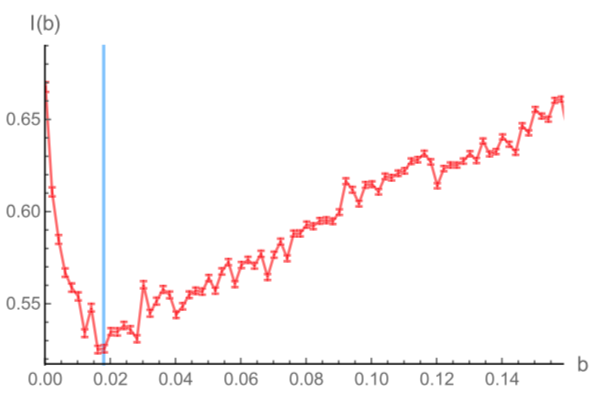
- Buses of Cuernavaca - an agent-based model for universal random matrix behavior minimizing mutual information
P. Warchoł, JOURNAL OF PHYSICS A: MATHEMATICAL AND THEORETICAL, 51, 265101, [arXiv:1709.10104].
The public transportation system of Cuernavaca, Mexico, exhibits random matrix theory statistics. In particular, the fluctuation of times between the arrival of buses on a given bus stop, follows the Wigner surmise for the Gaussian unitary ensemble. To model this, we propose an agent-based approach in which each bus driver tries to optimize his arrival time to the next stop with respect to an estimated arrival time of his predecessor. We choose a particular form of the associated utility function and recover the appropriate distribution in numerical experiments for a certain value of the only parameter of the model. We then investigate whether this value of the parameter is otherwise distinguished within an information theoretic approach and give numerical evidence that indeed it is associated with a minimum of averaged pairwise mutual information.
Funding
This research is funded by the Polish National Science Centre, through the project SONATA number 2016/21/D/ST2/01142.