This project is funded by a Sonata Bis grant of the Polish National Science Centre (NCN) under the grant number 2021/42/E/ST2/00234.

People

Principal Investigator: Dr. Mario Flory

Postdoc: Dr. Aranya Bhattacharya

PhD students: Emiliano Rizza and Lavish

Topics

Quantum field theory is one of the central concepts in theoretical physics, however, in the strong coupling regime where perturbation theory is not reliable, few analytical approaches exist that help understand the physics of the system. One such approach is the so called Anti-de Sitter/Conformal Field Theory correspondence (AdS/CFT) or gauge/gravity duality. As a concrete realisation of the more general concept of holography, this duality posits that certain strongly coupled quantum field theories (the "boundary") can be described in a mathematically equivalent way in terms of weakly coupled gravitational theories in higher dimensions (the "bulk"). It is hence a powerful concept that allows translating questions concerning one of these fields into the language of the other, where a new perspective on the problem can be gained, or where different mathematical methods may be at one's disposal.

The importance of this "holographic duality" is that it allows to derive predictions which are expected to be universal for strongly coupled quantum matter. This shows that holography as a general concept can help understanding real-world systems, or conversely, that real world systems can have properties that are holographic in nature. The overarching goal of this project will be to understand how holographic dualities can arise as a form of emergent gravity in strongly coupled states of matter, and how this in turn can help our understanding of such forms of matter. Specifically, we will deal with the following topics:

Applications of AdS/CFT to strongly coupled systems

AdS/CFT models lend themselves to applications to strongly coupled systems because they implement a duality between a weakly coupled bulk theory and a strongly coupled boundary theory. An important aspect of these applications, even in nonequilibrium situations, is universality, i.e. the fact that many phenomena observed in strongly coupled systems are qualitatively independent of their precise realisation at the level of underlying degrees of freedom.

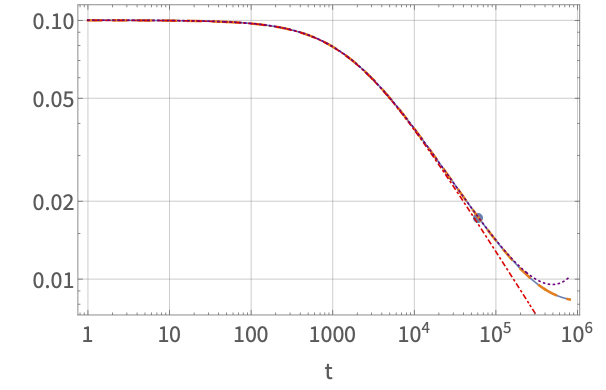
For example, in our recent paper Critical and near-critical relaxation of holographic superfluids we numerically studied exactly critical and near-critical quenches in holographic models of superconductors. We found that these systems relax towards their new equilibrium state in a way that exhibits a discrete type of scale invariance.

We further proposed a phenomenological Landau-Ginzburg like equation which, after numerically fixing its free parameters, was able to provide analytic predictions for the behaviour of the system not just at late, but even at early and intermediate times.

Fundamental aspects of the holographic principle

The AdS/CFT correspondence can be interpreted as giving rise to a form of emergent gravity, and holographic conceptions have often played a role in proposing more general scenarios of emergent gravity. In the AdS/CFT correspondence specifically, it has been demonstrated that Einstein’s equations in the bulk can be mathematically derived from the so-called first law of entanglement in the boundary theory.

Quantum information aspects of holography

The crucial role of boundary entanglement in the derivation of Einstein’s equations mentioned above is not coincidental, in fact aspects of quantum information theory lie at the very heart of the AdS/CFT correspondence. This result is based on the famed Ryu-Takayanagi (RT) formula which states that entanglement entropy of the dual theory (a measure of entanglement) is exactly encoded in the areas of certain extremal hypersurfaces embedded in the bulk spacetime, generalising the Bekenstein-Hawking formula for black hole entropy. This means that at least aspects of the bulk geometry can be reconstructed from boundary entanglement data. Certain inequalities of entanglement entropy that are automatically satisfied by systems for which the RT formula holds, forming the ”holographic entropy cone”, were later derived. This cone is only a subset of the more general ”quantum entropy cone”, a set of inequalities of entanglement entropy that any quantum system can be proven to obey. Hence these inequalities allow checking whether a given quantum state can in principle have a holographic description in terms of the RT formula or if it lies outside of the holographic entropy cone and can thus not have such a holographic description.

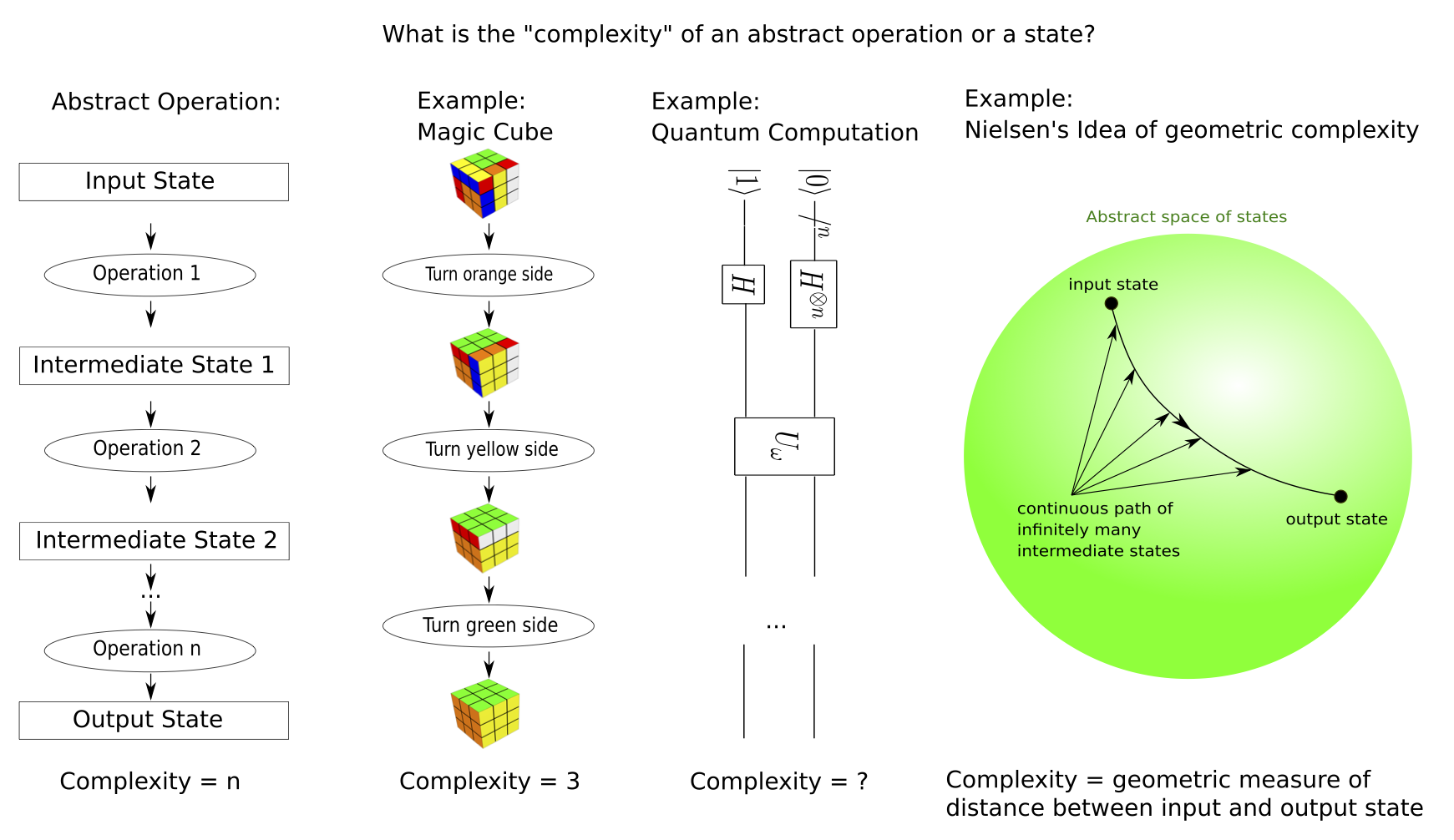
Another recent development concerns the idea that a measure of complexity of a field theory state could be calculated by holographic methods. In quantum information theory, especially assuming finite dimensional Hilbert spaces, measures of complexity have been introduced as notions of geodesic distances on group manifolds. On the quantum field theory side of the holographic duality, complexity is conjectured to be a notion of distance between the CFT state and a simple reference state, however, concrete tractable calculations along these lines are mostly restricted to free field theories. In the bulk, the ability to compute such measures of complexity is important as it may give insight into the storage and scrambling of information by black holes.

List of Publications

- M. Flory, S. Grieninger, S. Morales-Tejera; Critical and near-critical relaxation of holographic superfluids